转载声明：文章来源https://blog.csdn.net/Snowing1234_5/article/details/89350857

一、快速排序

最常用的排序算法，速度通常也是最快的。

时间复杂度：O（nlogn）

最坏：O（n^2）

空间复杂度：O（nlgn）

不稳定（比如 5 3 3 4 3 8 9 10 11 这个序列，在中枢元素5和3交换就会把元素3的稳定性打乱）

实现原理：

快排主要是通过选择一个关键值作为基准值。比基准值小的都在左边序列（一般是无序的），比基准值大的都在右边（一般是无序的）。依此递归，达到总体待排序序列都有序。

（1） 一次循环：从后往前比较，用基准值和最后一个值比较，如果比基准值小的交换位置，如果没有继续比较下一个，直到找到第一个比基准值小的值才交换。

（2） 找到这个值之后，又从前往后开始比较，如果有比基准值大的，交换位置，如果没有继续比较下一个，直到找到第一个比基准值大的值才交换。

（3）直到从前往后比较数组下标大于从后往前比较的数组下标值，结束第一次循环，此时，对于基准值来说，左右两边就是有序的了。

（4）接着分别比较左右两边的序列，重复上述的循环。

快速排序算法分析：

（1）快速排序的时间性能取决于快速排序递归的深度，可以用递归数来描述算法的执行情况。

（2）如果递归数是平衡的，那么此时的性能也是最好的。在最优的情况下，快排序算法的时间复杂度为O(nlogn)。

（3）就空间复杂度来说，主要是递归造成的堆空间的使用，最好情况，递归树的深度 log2n ，其空间复杂度也就为 O(logn) ，最坏情况，需要进行递归调用，其空间复杂度为 O(n)，平均情况空间复杂度也为 (logn)。

（4）关键字的比较和交换是跳跃进行的，因此，快速排序是种不稳定的排序方法。

二、堆排序

时间复杂度：O（n*logn）

特别适用于数据量很大的场合（百万级数据）。因为快排和归并排序都是基于递归的，数据量很大的

情况下容易发生堆栈溢出。

排序速度略低于快排。

也是一种不稳定的排序算法。比如 3 27 27 36，如果堆顶3先输出，则第三层（最后一个27）跑到堆顶，然后堆稳定，继续输出堆顶，是刚才那个27， 这样说明后面的27先于第二个位置的27输出，不稳定。

简单介绍：

堆排序是指利用堆这种数据结构进行设计的一种排序算法。堆排序利用了大根堆(或小根堆)堆顶记录的关键字最大(或最小)这一特征，使得在当前无序区中选取最大(或最小)关键字的记录变得简单。

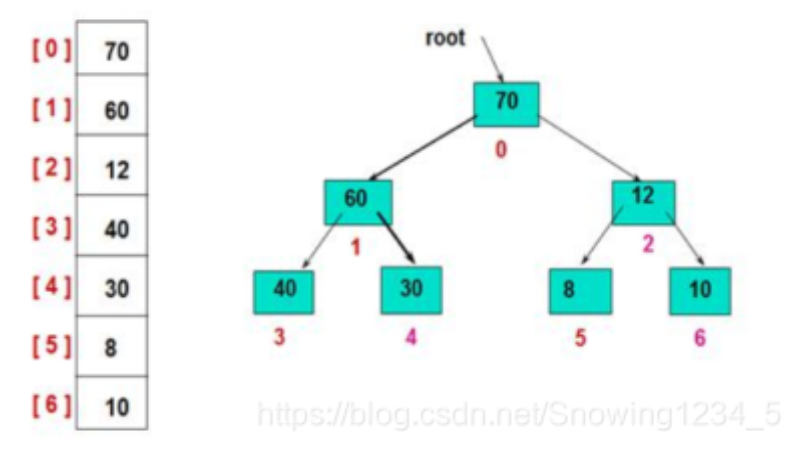
①堆是一棵顺序存储的完全二叉树。完全二叉树中所有非终端节点的值均不大于（或不小于）其左、右孩子节点的值。

②其中每个节点的值小于等于其左、右孩子的值，这样的堆称为小根堆；

③其中每个节点的值大于等于其左、右孩子的值，这样的堆称为大根堆；

实现原理：

将数组构造成初始堆（若想升序则建立大根堆，若想降序，则建立小根堆）从最后一个节点开始调整，得到初始堆。

先构造出来大根堆（假设从小到大排序），然后取出堆顶元素（也就是最大的元素），放到数组的最后面，然后再将剩余的元素构造大根堆，再取出堆顶元素放到数组倒数第二个位置，依次类推，直到所有的元素都放到数组中，排序就完成了

如下图所示：

三、二者之间的效率比较：

1、在数组长度小于一千万的时候，如下图，快速排序的速度要略微快于归并排序，可能是因为归并需要额外的数组开销（比如声明临时local数组用来储存排序结果），这些操作让归并算法在小规模数据的并不占优势

2.但是，当数据量达到亿级时，归并的速度开始超过快速排序了，如下图，因为归并排序比快排要稳定，所以在数据量大的时候，快排容易达到O(n^2)的时间复杂度，当然这里是指未改进的快排算法。

四、具体代码实现

package com.tulun.src1.work;

public class sort {
    public static void main(String[] args){
        //定义整型数组
        int[] arr = {12,20,5,16,15,1,30,45};
        //调用堆排序数组
        //HeapSort(arr);
        quickSort(arr);
        //输出排序后的数组
        for(int i=0;i<arr.length;i++) {
            System.out.print(arr[i]+"  ");
        }
    }

    /**
     * 堆排
     * @param arr
     */
    public static void HeapSort(int[] arr) {
        int n = arr.length-1;
        for(int i=(n-1)/2;i>=0;i--) {
            //构造大顶堆，从下往上构造
            //i为最后一个根节点，n为数组最后一个元素的下标
            //根据完全二叉树的性质，左右孩子节点分别为a[2*i+1],a[2*i+2] 也就是最后一个元素下标n=2*i+1
            HeapAdjust(arr,i,n);
        }
        for(int i=n;i>0;i--) {
            //把最大的数，也就是顶放到最后
            //i每次减一，因为要放的位置每次都不是固定的
            swap(arr,i);
            //再构造大顶堆
            HeapAdjust(arr,0,i-1);//-1防止越界
        }
    }

    //构造大顶堆函数，parent为父节点，length为数组最后一个元素的下标
    public static void HeapAdjust(int[] arr,int parent,int length) {
        //定义临时变量存储父节点中的数据，防止被覆盖
        int temp = arr[parent];
        //2*parent+1是其左孩子节点
        for(int i=parent*2+1;i<=length;i=i*2+1) {
            //如果左孩子大于右孩子，就让i指向右孩子
            if(i<length && arr[i]<arr[i+1]) {
                i++;
            }
            //如果父节点大于或者等于较大的孩子，那就退出循环
            if(temp>=arr[i]) {
                break;
            }
            //如果父节点小于孩子节点，那就把孩子节点放到父节点上
            arr[parent] = arr[i];
            //把孩子节点的下标赋值给parent
            //让其继续循环以保证大根堆构造正确
            parent = i;
        }
        //将刚刚的父节点中的数据赋值给新位置
        arr[parent] = temp;
    }
    //定义swap函数
    //功能：将根元素（堆顶）与最后位置的元素交换
    //注意这里的最后是相对最后，是在变化的
    public static void swap(int[] arr,int i){
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;
    }


    /**
     * 快排
     * @param arr
     * @param low
     * @param high
     * @return
     */
    private static int partition(int[] arr,int low,int high){
        int temp=arr[low];
        while(low<high){
            while(low<high && arr[high] > temp){
                high--;
            }
            if(low==high){
                break;
            }
            else{
                arr[low]=arr[high];
            }
            while(low < high && arr[low] <= temp){
                low++;
            }
            if(low==high){
                break;
            }
            else{
                arr[high]=arr[low];
            }
        }
        arr[low]=temp;
        return low;
    }
    private static void quick(int[] arr,int low,int high){
        int part = partition(arr, low, high);
        if(low+1 < part){//左边有数据
            quick(arr, low, part-1);
        }
        if(part+1 < high){//右边有数据
            quick(arr,part+1,high);//part 基准下标不需要再排，基准左边比基准小，右边比基准大
        }
    }
    public static void quickSort(int[] arr){
        quick(arr,0,arr.length-1);
    }
}