转载声明:文章来源https://blog.csdn.net/Starc_/article/details/134668002
前言
众所周知,我们在进行Java程序编写过程中,思路是很重要的一部分。在有了思路后,我们将用敲代码的方式将这一思路体现出来。以leetcode网站上的内容为例,我们可以看到在解题通过的同时,力扣还给出了两个重要的指标:执行用时分布和消耗内存分布。即编译运行程序所需要的时间和内存大小。

这两项指标是计算算法效率的两种分析方式。
在算法效率分析中称之为时间效率(时间复杂度)和空间效率(空间复杂度)。
经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度,所以我们如今已经不需要再特别关注一个算法的空间复杂度。
我们通常以时间复杂度作为优先级衡量一个算法的好坏。一、时间复杂度
基础计算
在一个算法运行过程中,每个语句中代码执行次数与系统整体运行时间成正比。语句执行次数越多,代码运行时间越长。因此引入了大O渐进表示法对时间复杂度进行简单的概括。
以下面的代码为例
public class Test1 {
public static void func1(int N){
int count = 0;
for (int i = 0; i < N ; i++) {
for (int j = 0; j < N ; j++) {
count++;
}
}
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}
public static void main(String[] args) {
func1(10);
}
}很简单的一段代码,从这段代码中,我们可以知道的推断count在第一个for循环中的执行次数为nn=n^2;在第二个循环中,执行次数为2N次;在最后while循环中,执行了10次。
因此,我们可以看出执行次数最多的语句相加起来的次数总和为(n^2+2n+10)。
我们定义函数F(n)对这个算式进行接收。(之后以F(n)代替)
具体计算规则
在F(n)中,随着变量n逐渐递增,在函数中有部分值是对函数最终答案影响是忽略不计的、可以省略的。
因此:在实际中我们计算时间复杂度时,并不一定要计算精确的执行次数,而只需要大概执行次数。
我们给出三条规则:
1、用常数1取代运行时间中的所有加法常数
2、在修改后的运行次数函数中,只保留最高阶项
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶
因此,上述例子中F(n)的时间复杂度表示为O(N^2)。
时间复杂度分为三种,最好情况、平均情况、最坏情况。
在普遍情况下,我们计算时间复杂度通常以***代码最坏情况下(执行次数最多)***表达计算结果。
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
二、几个例子
example1
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}在本题中,我们可以知道执行次数F(N)=2*N+10
根据三条规则中可以得到时间复杂度为O(N)
example2
void func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; k++) {
count++;
}
for (int k = 0; k < N ; k++) {
count++;
}
System.out.println(count);
}在本题中,我们可以知道存在M、N两个变量,其中,在第一个for循环中,count执行了M次,在第二个for循环中,count执行了N次,因此总共执行次数为(M+N)次,时间复杂度为O(M+N)。
example3
void func4(int N) {
int count = 0;
for (int k = 0; k < 100; k++) {
count++;
}
System.out.println(count);
}在本题中,定义了变量N,而在for循环中,k执行的次数为100次,这与变量N是无关的,本次执行次数为常数,因此时间复杂度为O(1)
example4(冒泡排序)
void Swap(int[] array,int n,int m){
int tmp = array[n];
array[n] = array[m];
array[m] = tmp;
}
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if(!sorted) {
break;
}
}
}冒泡排序法中,我们设array.length=N,end的变化范围为1~N,随着end的改变,
内部for循环执行次数为(n-1)+(n-2)+……+2+1 = (n^2-n)/2
因此时间复杂度为O(N^2)
最好情况下的时间复杂度:O(N) ->至少遍历一遍
example5(二分查找)
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}我们知道,进行二分查找的过程中我们需要在n个数据中找到我们需要的数据。每次都是对半进行查找。
因此,我们可以简化为F(N)=n*(1/2)^x 。而以最坏的情况进行计算,那么就是当N=1的时候我们才会找到所需要的数据。
所以:F(N)=1 x=log2^n. 时间复杂度O(log2(n))
example6(递归)
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N;
}在本题递归方法中,我们可以看到return后的三目运算符只是对N进行了一次判断,而不是在return语句中存在内置循环,因此每次return执行次数为1;而在return执行后,不满足N<2之后方法就会进行递归,直到N<2也就是N=1.因此我们可以知道在这个递归方法中递归的次数为N。因此时间复杂度为O(N)。
tips:在部分递归题中,时间复杂度O(N)=递归的次数*每次递归后执行的次数。那么在本题中
O(N)=N*1=Nexample7(斐波那契数列)
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}我们先看return语句,与上一题同样的三目运算符,因此执行次数为1.

我们可以浅显的看出第一层为1,第二层为2,第三层为4……
而这时候存在一个问题:并不是所有的节点都会到F(1)这一层,有的早早就已经结束了。那么归纳为2^(n-1)是否是合理的呢?
答案是合理的。我们知道,在计算时间复杂度的时候我们是计算总数的大概,那么在最后一层中,少了部分数是不影响时间复杂度的计算的。
因此,时间复杂度O(N)=2^n(等比数列求和)
三、空间复杂度
空间复杂度相对时间复杂度要简单许多。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。
以冒泡排序法为例
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
} if
(sorted == true) {
break;
}
}
}在这个方法中,并没有向系统申请新的内存,因此空间复杂度为O(1).
如果这时候向系统申请new一个新的数组,则空间复杂度将会上升至O(N)总结
经过科普和部分习题的计算,对时间复杂度和空间复杂度有了新的认知。
在计算复杂度的时候,我们应该结合代码的实现进行计算,而不是看到一个for循环直接N,这是不明智的做法。
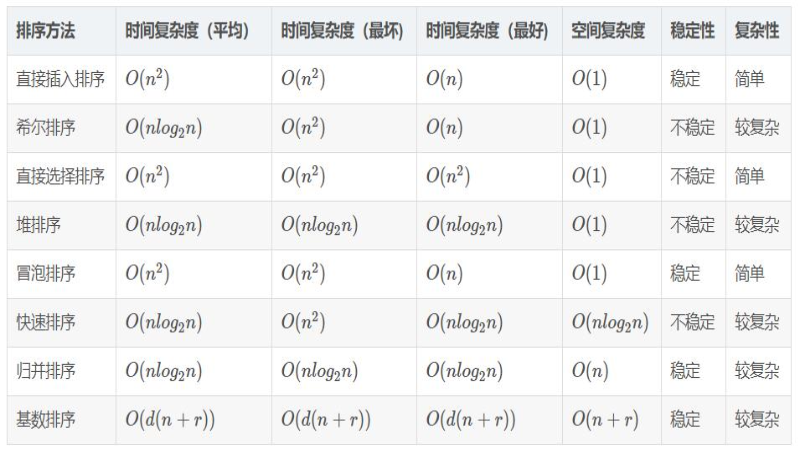
一些常用的时间复杂度:O(logN) O(N) O(N^2) O(1)
在代码的实现中,我们应当尽量减少不必要的空间冗余,这在提升时间速度和空间速度上会有许多显著的提升!



帖子还没人回复快来抢沙发